Die Kontaktpunktproblematik in der Unfallrekonstruktion - Energie-Doppelring- und Drehimpuls-Spiegel-Verfahren

Aus Colliseum
Zur Navigation springen Zur Suche springen

1991, pp. 259 – 263 (#9)

In der Unfallmechanik ist es üblich, die zeitlich ausgedehnte Kollision mit flächiger Berührung als Stoß unendlich kurzer Zeitdauer mit punktueller Berührung zu idealisieren. In dem vorliegenden Aufsatz wird der Einfluß dieser Idealisierung insbesondere bei der Anwendung des Drallsatzes auf die Fahrzeug-Fahrzeug-Kollision näher untersucht. Anschließend werden zwei neue Verfahren vorgestellt, die die Definition eines idealisierten Kontaktpunktes entbehrlich machen.


Considering crash-mechanics it is a common approach to idealise the temporal extended collision with surface contact by an impact of infinite short time with one-point-contact. In this paper the influence of this idealisation especially on the application of the conservation of angular momentum to vehicle-vehicle-collisions is discussed. At the end we present two new methods which make the definition of an idealised point of contact dispensable.

Zitat

Schimmelpfennig, K.-H.; Hebing, N.: Die Kontaktpunktproblematik in der Unfallrekonstruktion - Energie-Doppelring- und Drehimpuls-Spiegel-Verfahren. Verkehrsunfall und Fahrzeugtechnik 29 (1991), pp. 259 – 263 (#9)

Inhaltsangabe

Es werden zwei grafische Verfahren vorgestellt, die Energie- und Drallsatz in einer Weise anwenden, dass die Definition eines Kontaktpunkts entbehrlich wird. Bei der Anwendung des Energiesatzes werden darüber hinaus alle Annahmen betreffend Anstoßkonstellation und Stoßfaktor entbehrlich; stattdessen fließt vektorielle Trennungsgeschwindigkeit [math]\displaystyle{ \Delta \vec v' = \vec v_2' - \vec v_1' }[/math] in die Rechnung ein. Dies erlaubt die Anwendung des Verfahrens auch bei streifenden Stößen, wenn der Stoßfaktor nicht mehr sinnvoll eingegrenzt werden kann, wie in der Veröffentlichung an einem Unfallbeispiel illustriert.

Die Verfahren wurden bereits Jahre zuvor in Mathematische Grundlagen und Arbeitsverfahren für die Kollisionsmechanik im forensischen Bereich erarbeitet. Anlässlich von Der Einfluß der Kontaktpunktlage beim Drall-Spiegelverfahren - das kontaktpunktvariierte Drallfeld wurden diese Verfahren für eine Veröffentlichung aufgearbeitet.

Für die Berechnungen und Darstellungen in der Veröffentlichung wurde eine spezielle Version des Programms WinKol verwendet, die Wilhelm Deppe eigens für diese Veröffentlichung programmiert hatte (und dafür leider nur in einer Fußnote gewürdigt wird).

Anmerkungen

Anmerkungen von Plankensteiner

"verhakter" Stoß

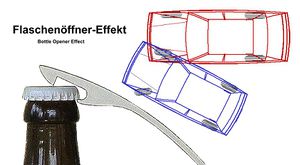
Nachdem Wilhelm Deppe im Heft 3/1991 über Probleme durch den Einfluss der Kontaktpunktlage im Zusammenhang mit dem von Schimmelpfennig entwickelten Drall-Spiegelverfahren berichtet hatte, ist dieser nur sechs Monate später erschienene Beitrag offenkundig ein (eilig) erstellter Lösungsvorschlag. Dabei liegt das Problem keineswegs bei dem Lösungsverfahren selbst, sondern vielmehr an dem ebenen Ersatzmodell mit einem während der Stoßzeit unveränderlichen Stoßpunkt, an dem die resultierende Stoßkraft angreift, und wie das nebenstehend dargestellte Schema eines (echten) verhakten Stoßes nach dem Prinzip eines Flaschenöffners zeigt, befindet sich der Stoßpunkt bei diesem Fall infolge der "Zugkräfte" zwischen den Vorderrädern außerhalb des Kontaktbereiches! Das eigentliche Problem ist der gewählte Begriff Kontaktpunkt, welcher einen Punkt innerhalb des Kontaktbereiches suggeriert.

Auch wenn es sich beim Flaschenöffnereffekt um einen sehr seltenen Sonderfall handelt (der in 35 Jahren singulär geblieben ist), es gibt noch eine Reihe weiterer Fälle (bspw. hier) bei denen das "übliche" Ersatzmodell nicht angewendet werden kann. Es ist daher keine echte Lösung des Problems, wenn auf dem gleichen Modell aufbauend bei ausreichenden Angaben die mathematische Überbestimmtheit des Gleichungssystems dazu benutzt wird, durch Umformungen der Gleichungen den Stoßpunkt zu verstecken, auch wenn diese Vogel Strauß Politik in Sonderfällen zu brauchbaren Lösungen führen kann.

Der Versuch die Ableitung der Gleichungen nachzuvollziehen gelang nur bis zur Gleichung (13), in der irgendetwas verloren gegangen sein muss; vielleicht kann die ausführliche und vollständige Ableitung dieser Gleichung hier nachgereicht werden.

Richtigstellung von Hugemann, W.

Was den eilig erstellten Lösungsvorschlag betrifft, liegt Kollege Plankensteiner falsch, siehe oben. Herr Schimmelpfnnig hat die Veröffentlichung von Deppe nur zum Anlass genommen, mich zu bitten, die dortigen Darlegungen zu einer Veröffentlichung auszuarbeiten.

Gleichung (13) fällt in der Veröffentlichung in der Tat ein wenig vom Himmel, ist in der Herleitung jedoch nicht weiter schwer. Wir schreiben den Energiesatz am besten in der Form

[math]\displaystyle{ m_1 (v_1^2-v_1'^2) + m_2 (v_2^2-v_2'^2) = 2 \Delta E_t }[/math]

mit [math]\displaystyle{ \Delta E_t }[/math] als Verlust an translatorischer kinetischer Energie, der den »Verlust« durch die stoßbedingte Umwandlung von Bahndrall in Eigendrall einschließt. Mit der Definition des Stoßantriebs können wir die Einlaufgeschwindigkeiten eliminieren

[math]\displaystyle{ \vec v_1 = \vec v_1' - \frac 1 {m_1} \vec S }[/math]

und damit

[math]\displaystyle{ v_1^2 = \left(\frac 1 {m_1} \vec S - \vec v_1'\right) \cdot \left(\frac 1 {m_1} \vec S - \vec v_1'\right) = \frac 1 {m_1^2} S^2 + v_1'^2 - \frac 1 {m_1} \vec S \cdot \vec v_1' }[/math]

oder

[math]\displaystyle{ m_1 (v_1^2 -v_1'^2) = \frac 1 {m_1} S^2 - \vec S \cdot \vec v_1' }[/math]

und analog für [math]\displaystyle{ v_2 }[/math], sodass sich in der Summe

[math]\displaystyle{ \frac 1 {m_1} S^2 - \vec S \cdot \vec v_1' + \frac 1 {m_2} S^2 + \vec S \cdot \vec v_2' = \frac 1 {m^*} S^2 - 2 \vec S \cdot \Delta \vec v' = 2 \Delta E_t }[/math]

ergibt, was identisch mit Gl. (13) ist.

In der Veröffentlichung wird anstelle von [math]\displaystyle{ S^2 }[/math] stets [math]\displaystyle{ \vec S^2 }[/math] geschrieben, was [math]\displaystyle{ \vec S \cdot \vec S }[/math] bedeutet und damit dasselbe ist. Das Skalarprodukt [math]\displaystyle{ \vec S \cdot \Delta \vec v' }[/math] ist in der Veröffentlichung ohne Punkt geschrieben.

Multiplizieren mit der relativen Masse

[math]\displaystyle{ m^*=\frac {m_1\,m_2}{m_1+m_2} }[/math]

und quadratisches Ergänzen ergibt dann

[math]\displaystyle{ S^2 - 2 m^* \vec S \cdot \Delta \vec v' + (m^* \Delta \vec v')^2 = 2 \, m^* \Delta E_t + (m^* \Delta \vec v')^2 }[/math]

und damit

[math]\displaystyle{ (\vec S - m^* \Delta \vec v')^2 = 2 \, m^* \Delta E_t + (m^* \Delta \vec v')^2 }[/math]

Im Falle [math]\displaystyle{ \Delta \vec v' = \vec 0 }[/math] ergibt sich

[math]\displaystyle{ S_0 = \sqrt{2 \, m^* \Delta E_t} }[/math]

sodass man auch

[math]\displaystyle{ (\vec S - m^* \Delta \vec v')^2 = S_0^2 + (m^* \Delta \vec v')^2 }[/math]

schreiben kann.

Hinweis 1: Im Falle von Drehungen ist [math]\displaystyle{ \Delta \vec v' = \vec 0 }[/math] kein plastsicher Stoß, denn gleiche Schwerpunktgeschwindigkeiten führen durch die Drehungen auf unterschiedliche Kontaktpunktgeschwindigkeiten.

Hinweis 2: [math]\displaystyle{ m^* }[/math] bezeichnet hier, wie man obiger Definition entnimmt, die »normale« relative Masse und nicht etwa die reduzierte relative Masse, wie sie analog aus den jeweils reduzierten Massen [math]\displaystyle{ \bar m_i }[/math] berechnet wird. Das ist insofern bemerkenswert, als dass über die reduzierte relative Masse wieder implizit auf die Anstoßkonstellation Bezug genommen würde. Insofern ist die hier vorgestellte Version des Energiesatzes tatsächlich frei von irgendwelchen Annahmen betreffend die Anstoßkonstellation.

Hinweis 3: Die Bezeichnung »Energie-Doppelring-Verfahren« ist eigentlich falsch. Es gibt nur einen Kreis oder Ring, über den der Betrag des Stoßantriebs abhängig von seiner Richtung definiert wird. Der Stoßantrieb für Fzg 2 ist schlicht dessen Gegenvektor [math]\displaystyle{ -\vec S }[/math], und man kann sich das Spiegeln des Energierings sparen. Der Überlappung der Ringe kommt keine Bedeutung zu. Entsprechend wird in der GeoGebra-Konstruktion auf den zweiten Energiering (bzw. Kreis) verzichtet.

Umsetzung in GeoGebra

GeoGebra-Projekt: Energie-Doppelring-Verfahren

Um rein mit Impulsvektoren arbeiten zu können, muss der Vektor [math]\displaystyle{ \Delta v' }[/math] durch die Auslaufimpulse beschrieben werden:

[math]\displaystyle{ m^* (\vec v_2' - \vec v_1') = \frac{m_1\,m_2}{m_1+m_2} \left( \frac 1 {m_2} \vec p_2' - \frac 1 {m_1} \vec p_1'\right)= \frac 1 {1 + \mu} (\vec p_2' - \mu \,\vec p_1') }[/math]

mit [math]\displaystyle{ \mu = m_2/m_1 }[/math].

Der Trennungsimpuls [math]\displaystyle{ \vec p'=\vec p_2' - \vec p_1' }[/math] und die Trennungsgeschwindikeit [math]\displaystyle{ \vec v'=\vec v_2' - \vec v_1' }[/math] sind nur im Falle µ = 1 kollinear, haben also im Regelfall also unterschiedliche Richtungen.

Die quadratische Addition [math]\displaystyle{ S_0^2 + (m^* \Delta \vec v')^2 }[/math] wird in Der GeoGebra-Konstruktion über eine rechtwinklige Dreieckskonstruktion ausgeführt, indem der Kreis mit dem Radius [math]\displaystyle{ S_0 }[/math] mit dem Strahl senkrecht zum Ortsvektor [math]\displaystyle{ m^* \Delta \vec v' }[/math] des Kreismittelpunkts zum Schnitt gebracht wird.

Wie unterhalb der GeoGebra-Konstruktion erläutert, wird auf das Spiegeln zum Doppelkreis (bzw. -ring) verzichtet, weil den Schnittpunkten (bzw. -flächen) der Kreise (bzw. Ringen) keine Bedeutung zukommt, sodass man besser schlicht den Stoßantrieb spiegelt.

Formelwerk

Das Originalformelwerk aus der Veröffentlichung lautet:

Gl. (1) Impulserhaltung: [math]\displaystyle{ m_1 (\vec v - \vec v_1') = -m_2 (\vec v_2 - \vec v_2') }[/math]

Gl. (2) Energieerhaltung: [math]\displaystyle{ m_1 (v_1^2 - v_1'^2) + \Theta_1 (\omega_1^2 - \omega_1'^2) - \Delta E = -m_2 (v_2^2 - v_2'^2) - \Theta_2 (\omega_2^2 - \omega_2'^2) + \Delta E }[/math]

Gl. (3) Drallsatz: [math]\displaystyle{ m_1 (\vec r_1 \times \vec v_1 - \vec r_1' \times \vec v_1') + \Theta_1 (\vec \omega_1 - \vec \omega_1') = -m_2 (\vec r_2 \times \vec v_2 - \vec r_2' \times \vec v_2') - \Theta_2 (\vec \omega_2 - \vec \omega_2') }[/math]

Gl. (4): [math]\displaystyle{ \frac{1}{v_1} \vec v_1 = \vec e_1, \quad \vec r_1 = \vec r_{10} = \vec r_1' }[/math] [math]\displaystyle{ ,\quad \frac{1}{v_2} \vec v_2 = \vec e_2, \quad \vec r_2 = \vec r_{20} = \vec r_2' }[/math]

Gl. (5): [math]\displaystyle{ \vec \omega_1 =0, \quad \vec \omega_2 =0 }[/math]

Gl. (6) Stoßantrieb: [math]\displaystyle{ \vec S_1 \doteq \vec S = -m_1 (\vec v_1 - \vec v_1') = \int_{0}^{t'} \vec F_1(t) dt }[/math]

Gl. (7) »Rotationsantrieb«: [math]\displaystyle{ \vec R_1 \doteq - \Theta_1 (\vec \omega_1 - \vec \omega_1') = \int_{0}^{t'} \overline{\vec p_1}(t) \times \vec F_1(t) dt }[/math]

Gl. (8): [math]\displaystyle{ \vec F_1 = \int_{\vec p_{1a}(t)}^{\vec p_{1b}(t)} \vec f_1(t, \vec p_1) dp_1 }[/math]

Gl. (9): [math]\displaystyle{ \overline{\vec p_1}(t) \times \vec F_1(t) = \int_{\vec p_{1a}(t)}^{\vec p_{1b}(t)} \vec p_1(t) \times \vec f_1(t, \vec p_1) dp_1 }[/math]

Gl. (10): [math]\displaystyle{ \vec p_{1k} \times \int_{0}^{t'} \vec F_1(t) dt = \int_{0}^{t'} \overline{\vec p_1}(t) \times \vec F_1(t) dt = \int_{0}^{t'} \int_{\vec p_{1a}(t)}^{\vec p_{1b}(t)} \vec p_1(t) \times \vec f_1(t, \vec p_1) dp_1 \; dt }[/math]

Gl. (11): [math]\displaystyle{ - \Theta_1 (\vec \omega_1 - \vec \omega_1') = \vec p_{1k} \times \int_{0}^{t'} \vec F_1(t) dt = \vec p_{1k} \times \vec S }[/math]

Gl. (12): [math]\displaystyle{ \vec p_{1k} - \vec p_{2k} = \vec r_{2k} - \vec r_{1k} \doteq \vec p_k }[/math]

Gl. (13) (aus (2), (1), (6) und (14)): [math]\displaystyle{ \frac{\vec S^2}{m^*} - 2 \vec S \Delta \vec v' = 2 \Delta E + \Theta_1 (\omega_1'^2 - \omega_1^2) + \Theta_2 (\omega_2'^2 - \omega_2^2) }[/math]

Gl. (14): [math]\displaystyle{ \Delta \vec v' \doteq \vec v_1' - \vec v_2' }[/math]

Gl. (15): [math]\displaystyle{ (\vec S - m^* \Delta \vec v')^2 = m^* [2 \Delta E + \Theta_1 (\omega_1'^2 - \omega_1^2) + \Theta_2 (\omega_2'^2 - \omega_1^2) + m^* \Delta \vec v'^2] }[/math]

Gl. (16): [math]\displaystyle{ \vec M = m^* \Delta \vec v' }[/math]

Gl. (17): [math]\displaystyle{ R^2 = m^* [2 \Delta E + \Theta_1 (\omega_1'^2 - \omega_1^2) + \Theta_2 (\omega_2'^2 - \omega_2^2) + m^* \Delta \vec v'^2] }[/math]

Gl. (18) (aus (11) und (12): [math]\displaystyle{ \vec p_k \times \vec S = \Theta_1 (\vec \omega_1' - \vec \omega_1) + \Theta_2 (\vec \omega_2' - \vec \omega_2) }[/math]

Gl. (19): [math]\displaystyle{ S_\bot = \frac{\Theta_1 (\vec \omega_1' - \vec \omega_1) + \Theta_2 (\vec \omega_2' - \vec \omega_2)}{p_k} }[/math]


Anmerkungen (--Vdengineering (Diskussion) 20:23, 17. Dez. 2015 (CET)):

  • Gl. (1): hier fehlt wohl einmal der Index 1
  • Gl. (13): hier muss der geneigte Leser für das nicht eingeführte m* in VKU-Ausgabe #9 1982 auf die Suche gehen. m* wird dort als »relative Masse« eingeführt: [math]\displaystyle{ m^* = \frac{m_1 \cdot m_2}{m_1 + m_2} }[/math] Siehe dort auch »reduzierte relative Masse«.
  • Gl. (15): hier dürfte ein Index falsch sein.

Verfahren aus dem Hause Schimmelpfennig und Becke

Weitere Infos zum Thema

Abgerufen von „http:///wiki/index.php?title=Die_Kontaktpunktproblematik_in_der_Unfallrekonstruktion_-_Energie-Doppelring-_und_Drehimpuls-Spiegel-Verfahren&oldid=31630“