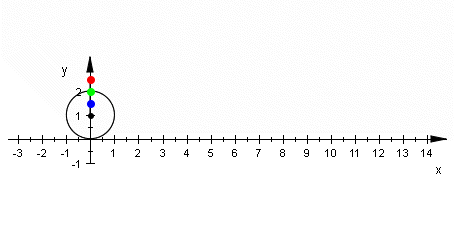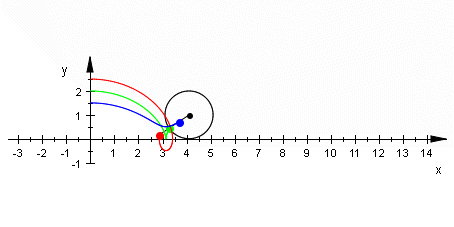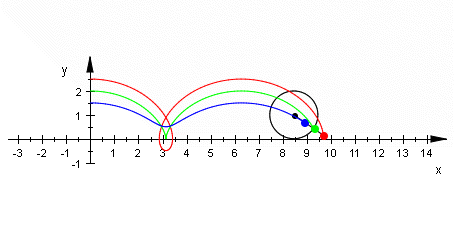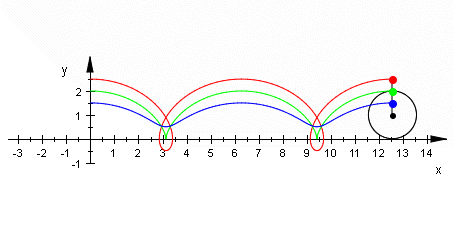Berechnung von Radandrehspuren
Calculation of traces of a cranking wheel
Theorie
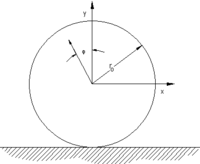
Die nebenstehende Abbildung zeigt die Bewegung eines beliebigen Punktes auf der Seite eines drehenden Rades. (Der Ursprung des Koordinatensystems liegt im Radzentrum.)
Schlupffreies Abrollen
Wir nehmen zunächst schlupffreies Abrollen des Rades an. Zum Zeitpunkt t = 0 befindet sich der Punkt am oberen Totpunkt der Bewegungsbahn auf der y-Achse. Dann gilt: [math]\displaystyle{ y = r \cos \varphi \\ x = v t + r \sin \varphi }[/math]
Der Radumfangsweg v t ergibt sich aus dem Produkt von Drehwinkel und Rollradius:
[math]\displaystyle{
x = R \varphi + r \sin \varphi
}[/math]
Zeichnet das Rad auf einem weiteren Fahrzeug, das sich mit der Geschwindigkeit v2 bewegt, so gilt:
[math]\displaystyle{
x_{\text {rel}} = (v - v_2) t + r \sin \varphi
}[/math]
bzw. mit dem Geschwindigkeitsverhältnis:
[math]\displaystyle{
z = \frac {v_{(1)}} {v_2} \left( \frac {\text {zeichnendes Fzg}} {\text {gestreiftes Fzg}} \right)
}[/math]
dann:
[math]\displaystyle{
x_{\text {rel}} = \left( 1 - \frac 1 z \right) R \varphi + r \sin \varphi
}[/math]
Die Herleitung findet sich etwa in "Die Aufklärung des Kfz-Versicherungsbetrugs".
Es sind
- r': der Radius des betrachteten Punktes
- R: der Außenradius des Rades
- φ: der Drehwinkel
- z: das Geschwindikeitsverhältnis der Fahrzeuge v1 / v2
Die Indizes sind dabei so vergeben, wie in der Unfallrekonstruktion zumeist üblich
- 1: stoßendes Fahrzeug (hier: zeichnendes Fahrzeug)
- 2: gestoßenes Fahrzeug (hier: Fahrzeug mit den Antragspuren)
Der Nullpunkt liegt bei obiger Formel im Radzentrum; legt man ihn auf die Fahrbahnoberfläche, ist bei der y-Koordinate r0 zu addieren.
Spurzeichnung Rad auf Rad
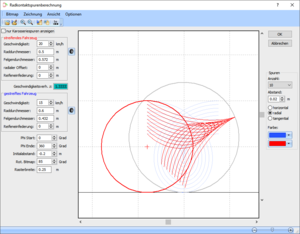
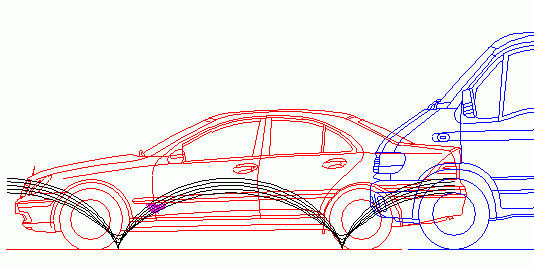
Die im letzten Abschnitt hergeleitete Beziehungen xrel(t), y(t) beschreiben letztlich die Bewegung des Radpunktes P in dem mit Fahrzeug 2 mitbewegten Bezugssystem. In diesem Bezugssystem haben die Räder von Fahrzeug 2 keine Lineargeschwindigkeit, sondern drehen sich ausschließlich um ihre Achse. Um die 'Karosseriekoordinaten' in das sich mit dem gestreiften Rad mitdrehende Koordinatensystem [math]\displaystyle{ x',y' }[/math] zu transformieren, muss also einzig die Drehung des Rades berücksichtigt werden. In Matrixschreibweise: [math]\displaystyle{ \begin{pmatrix} x'\\y' \end{pmatrix} = \begin{pmatrix} \cos \varphi_2 & \sin \varphi_2\\ -\sin \varphi_2 & \cos \varphi_2 \end{pmatrix} \begin{pmatrix} x_{\text{rel}}\\y \end{pmatrix} }[/math] mit: [math]\displaystyle{ \varphi_2 = \omega_2 \, t }[/math] Die Abbildung rechts zeigt mit PC-Crash berechnete Kontaktspuren Rad-auf-Rad, wobei die auf der Karosserie gezeichneten Spuren hellblau überlagert sind. (Dies ist nicht mit PC-Crash selbst möglich, sondern nur in der Bildbearbeitung.) Liegt der Beginn der Kontaktspuren (wie hier) innerhalb des Rads, auf dem gezeichnet wird, so haben die 'Karosseriekurven' und die auf dem Rad gezeichneten Kurven jeweils denselben Startpunkt.
Abrollen unter Schlupf
Bewegt sich das zeichnende Rad unter dem Bremsschlupf λ, etwa infolge einer ABS-Bremsung, so gilt: [math]\displaystyle{ \lambda = \frac {v - \omega \, R}{v} }[/math] bzw.: [math]\displaystyle{ v = \frac {\omega \,R}{1 - \lambda} }[/math] und für den Linearweg somit: [math]\displaystyle{ x = \frac 1 {1 - \lambda} R \varphi }[/math] Die entscheidende Gleichung ist damit folgendermaßen zu modifizieren: [math]\displaystyle{ x_{\text {rel}} = \frac 1 {1- \lambda} \left( 1 - \frac 1 z \right) R \varphi + r \sin \varphi }[/math] Radschlupf bewirkt also denselben Effekt wie eine Erhöhung des Geschwindigkeitsverhältnisses; man kann eine bestimmte Kombination aus Geschwindigkeitsverhältnis z2; λ damit auf ein äquivalentes Geschwindigkeitsverhältnis z1 umrechnen: [math]\displaystyle{ 1 - 1 / z_1 = \frac {1 - 1/z_2}{1-\lambda} }[/math] Nach kurzer Umformung ergibt sich: [math]\displaystyle{ z_1 = \frac {1-\eta}{1/z_2-\lambda} }[/math] Für [math]\displaystyle{ \eta = 0 }[/math] ergibt sich z1 = z2 und für die Kombination z2 = 2 ; [math]\displaystyle{ \lambda }[/math] = 0,1 ergibt sich z1 = 2,25.
Wird umgekehrt dasjenige Verhätnis z1 bestimmt, bei dem sich die berechneten Spuren mit den tatsächlichen decken (Vorgehensweise bei der Radkontaktspurenberechnung in PC-Crash), so lässt sich daraus umgekehrt das tatsächliche Geschwindigkeitsverhältnis z2 berechnen: [math]\displaystyle{ z_2 = \frac {z_1} {1 +(z_1 - 1) \lambda} }[/math]
"Abrollen" einer Fahrrad-Tretkurbel
Der Verlauf einer von einer Tretkurbel hinterlassenen Kontaktspur an der Seite eines (meist überholenden) Fahrzeugs lässt sich ebenfalls über die gewohnte Beziehung berechnen, wenn man das Geschwindigkeitsverhältnis mit der Gesamtübersetzung η umrechnet. Die Herleitung verläuft analog zu der unter Schlupf: [math]\displaystyle{ x = v t + r \sin \omega t }[/math] mit: [math]\displaystyle{ v = \frac N n \frac R r r \omega t = \eta r \omega t }[/math]
Mit
- N: Zähnezahl des aktuellen Kettenblatts
- n: Zähnezahl des aktuellen Ritzels
- R: Abrollradius der Laufräder
- r: Länge der Tretkurbel
und es ergibt sich: [math]\displaystyle{ x_{\text{rel}} = \eta \left( 1 - \frac 1 z \right) r \omega t + r \sin \omega t }[/math] und damit: [math]\displaystyle{ 1 - 1/z_1 = \eta \left( 1 - 1/z_2 \right) }[/math] und schließlich:
[math]\displaystyle{ z_1 = \frac 1 {1 - \eta ( 1 - 1 / {z_2})} }[/math]
Bei der Berechnung der Kontaktspuren ist dann zusätzlich noch die Höhe des Tretlagerwelle über Grund in Form eines Offsets in y-Richtung zu berücksichtigen.
Mit
- N = 38
- n = 23
- R = 35 cm
- r = 18,5 cm
ergibt sich η = 3,13. Fährt der Radfahrer z.B. mit v1 = 22,5 km/h und der Überholende mit v2 = 30 km/h, so ist z2 = 0,75 und z2 = 0,49.
Wird umgekehrt dasjenige Verhältnis z1 bestimmt, bei dem sich die berechneten Spuren mit den tatsächlichen decken (Vorgehensweise bei der Radkontaktspurenberechnung in PC-Crash), so lässt sich daraus umgekehrt das tatsächliche Geschwindigkeitsverhältnis z2 berechnen: [math]\displaystyle{ z_2 = \frac \eta {\eta - 1 + 1 / z_1} }[/math]
Starker Lenkeinschlag
In einem weiteren Spezialfall streift ein vorbeifahrendes Fahrzeug das ausgestellte Rad eines (meist deutlich langsamer) Abbiegenden / Wendenden. Im Gegensatz zu den bisher behandelten Fällen bewegen sich die Fahrzeuge jetzt nicht parallel, vielmehr bewegt sich das Rad nun auf die gestreifte Fläche zu, wodurch
- das Rad in den Unfallgegener eindringt und
- an der Drehbewegung gehindert wird, sodass der Schlupf im Laufe des Kontakts wächst.
Man wird in diesem Fall nur den Beginn der Radandrehspuren auswerten können. In diesem Fall gilt mit dem Radeinschlagwinkel α (die Fahrzeuge seien noch parallel ausgerichtet): [math]\displaystyle{ x = (v t + r \sin \omega t) \cos \alpha }[/math] und mithin: [math]\displaystyle{ x_{rel} = (v \cos \alpha - v_2) t + r \sin \omega t \cos \alpha = \left( \cos \alpha - \frac 1 z \right) r \varphi + r \sin \varphi \cos \alpha }[/math] während weiterhin: [math]\displaystyle{ y = r \cos \omega t = r \cos \varphi }[/math]
gilt. Der Lenkeinschlag beeinflusst nun sowohl die reine Linearbewegung als auch den zyklischen rotatorischen Anteil in x-Richtung. Betrachtet man die nur die zyklisch auftretenden Punkte, an denen: [math]\displaystyle{ \sin \varphi = 0 }[/math] gilt, so lässt sich zumindest der "Rhythmus" der Bahnkurven nachbilden. An diesen Punkten muss dann für ein äquivalents z2 gelten: [math]\displaystyle{ \cos \alpha - \frac 1 {z_2} = 1 - \frac 1 z }[/math] was auf die Umrechnung: [math]\displaystyle{ z_2 = \frac z {z (\cos \alpha -1) + 1} }[/math] führt. Dem nebenstehenden Excel-Diagramm liegt folgender Parametzersatz zugrunde:
- r = 0,3 m
- v1 = 5 km/h
- α = 60° (cos α = 0,5)
- v2 = 20 km/h (z = 0,25) ohne Lenkeinschlag
- v'2 = 17,5 km/h (z2 = 0,2857) mit Lenkeinschlag
(Die Umrechnung z → z2 ergibt sich aus obiger Beziehung.) Die Spurverläufe sind nicht exakt identisch, aber sehr ähnlich. Man kann also abermals eine konventionelle Radkontaktspurenberechnung in PC-Crash durchführt und das so ermittelte Geschwindigkeitsverhältnis auf das tatsächliche umrechnen.
Umsetzung als AutoSketch-Makro
Anwendung des Makros
Das unten gelistete AutoSketch-Makro zeichnet Polylinien mit den Bewegungsbahnen der Punkte zwischen Radinnenradius und Radaußenradius, ähnlich wie dies im entsprechenden Modul von PC-Crash 8.0 geschieht. Die Makrosprache von AutoSketch 2.1 ähnelt BASIC, sodass das Makro in ähnlicher Form auch in anderen CAD-Umgebungen schnell umgesetzt werden kann.
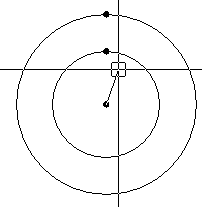
Um das Makro in AutoSketch zu verwenden kopiert man die Befehle in einen Editor und speichert es in einer Datei mit der Enden MCR (macro). Dann kann es im Menü "Einstellungen" mit der entsprechenden Schaltfläche abgespielt werden. Im Bild sind die entscheidenden Punkte beim Ausführen des Makros markiert:
Vor dem Ausführen des Makros muss man zunächst den Nullpunkt (Ursprung) der gesamten Zeichnung auf den Radmittelpunkt legen. (= Oben links auf den Schnittpunkt der Lineale klicken und dann den Radmittelpunkt bezeichnen.)
Anschließend hängt das Fadenkreuz (der Cursor) an einem "Gummiband" an diesem Ursprung; und man klickt "ganz oben" auf den Radinnenkreis. Danach macht man nochmals dasselbe für den Radaußenkreis.
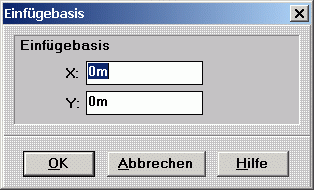
Danach erscheint das Dialogfeld Einfügebasis:
Für den Wert X gibt man das Geschwindigkeitsverhältnis z aus obiger Formel ein und für den Wert Y den Schlupf (Standardwert 0). Das Makro zeichnet dann die Radandrehspuren:
Das Makro zeichnet die Spuren standardmäßig von rechts nach links, wenn das zeichnende Fahrzeug schneller ist, so entspricht es der Orientierung der Fahrzeuge in den gängigen Symbolbibliotheken (in denen meist die Fahrerseite dargestellt ist). Diese Richtung kann ggf. durch Bearbeitung des Makro-Codes geändert werden, indem die Variable DIR (direction) auf 1 gesetzt wird.
Makro-Code
' AutoSketch 2.1 Makro zum Zeichnen von Radandrehspuren
' Der Nullpunkt der Zeichnung muss zuvor ins Radzentrum gelegt werden
'
' Fehlerschranke
eps = 0.0001
' Winkel-Inkrement
dphi = 0.1
' Endwinkel der Simulation in Radiant
Ende = 10 * /pi
' Umrechnungsfaktor in Radiant
deg = 57.52
' Anzahl der Streifen
Strips=5
' Richtung: -1 = von rechts nach links
dir = -1.0
' Wert wird später restauriert
OldPD = /PICKDELTA
'
' Radius des Randinnenrands
DrawLine
Point 0,0
UserInput
rmin = /ly
Undo
'
' Radius des Radaußenrands
DrawLine
Point 0,0
UserInput
r0 = /ly
Undo
'
' Angabe des Geschwindigkeitsverhältnisses
Set INSBASEX 0
Set INSBASEY 0
SetPartBase
UserInput
z = /INSBASEX
eta = /INSBASEY
'
dr = (r0-rmin) / (Strips-1)
r = rmin
' Auswahlbox auf Null setzen, damit die Polylinien nicht
' versehentlich beendet werden
Set PICKDELTA 0
Repeat
phi = 0
DrawPolyLine
Repeat
x = dir * (r0*(1-1/z) * phi / (1 - eta) + r*sin(deg*phi))
y = r*cos(deg*phi)
Point x,y
phi = phi + dphi
until phi > ende
Point /lpoint
r = r + dr
until r > r0 + eps
'
' Wert restaurieren
Set PICKDELTA OldPD
Veröffentlichungen im VKU
- 2001 #2 Zwei Versuche zur Problematik Radandrehspuren
- 2001 #7/8 Weitere Versuche zur Problematik der Radandrehspuren
- 2003 #6 Bewertung von Radkontaktspuren
- 2004 #1 Interpretation von Reifen-Kontaktspuren im gleichläufigen Verkehr
Weitere Infos zum Thema
- 1994 Theorie und Praxis der forensischen Unfallanalyse, Kapitel 4.9
- 1995 Die Aufklärung des Kfz-Versicherungsbetrugs, S. 258 – 261
- 2000 Experimentelle Untersuchung zur Bestimmbarkeit des Geschwindigkeitsverhältnisses zwischen den Kollisionspartnern aus den von der Seitenwand eines Reifen gezeichneten Aufriebspuren. Diplomarbeit, Technische Universität Berlin, Institut für Straßen- und Schienenverkehr.
- Berechnung von Radandrehspuren