Hinweise auf die Bedeutung der Fahrbahnquerneigung in der Unfallrekonstruktion
1986, p. 221 (#7)
Die Fahrbahnquerneigung kann in der Unfallrekonstruktion eine wichtige Rolle spielen. Diese Ausarbeitung erfaßt die seitliche Verlagerung, die unter dem Einfluß der Fahrbahnquerneigung auftritt, als Funktion der Ausgangsgeschwindigkeit und der Verzögerung. Außerdem wird auf ihre Bedeutung bei Bremsvorgängen und bei der Rekonstruktion von Pkw-Fußgänger bzw. Pkw-Zweiradunfällen hingewiesen.
The lateral inclination of the roadway may play an important role in the reconstruction of accidents. This elaboration takes into account the sideways displacement occurring under the influence of the lateral inclination of the roadway as a function of the original speed and the retardation. Its significance should also be pointed out in respects of braking processes and in the reconstruction of accidents involving cars and pedestrians or cars and two-wheeled vehicles.
Zitat
Schimmelpfennig, K.-H.; Rennich, D.: Hinweise auf die Bedeutung der Fahrbahnquerneigung in der Unfallrekonstruktion. Verkehrsunfall und Fahrzeugtechnik 24 (1986), pp. 221 – 223 (# 7/8)
Inhaltsangabe
Im ersten Teil des Beitrags wird der Einfluss der Fahrbahnquerneigung auf ein zunächst in Fahrbahnlängsrichtung rutschendes Objekt untersucht. Die Autoren stellen ein Differenzialgleichungssystem auf, das die Rutschbewegung in Fahrbahnlängs- und -querrichtung beschreibt. Diese Differenzialgleichungssystem kann unter der Annahme, dass der Bahnwinkel gegenüber der Fahrbahnlängsrichtung stets klein bleibt, analytisch gelöst werden. Die Autoren konzentrieren sich dabei vor allem auf den seitlichen Versatz in der Endlage, für den sich – bei Annahme Coulombscher Reibung – unter dieser Voraussetzung eine sehr einfache Beziehung ergibt.
Im zweiten Teil des Beitrags geht es dann vor allem um Anwendungsmöglichkeiten für die theoretisch abgeleitete Beziehung.
Ergänzung
Die Autoren versäumen es, vor der Lösung der DGLs den einfachsten aller Lösungsansätze vorzustellen, in dem man nämlich die Reibung in Querrichtung komplett vernachlässigt. In diesem Fall gilt
[math]\displaystyle{ \ddot y = g \, \sin \alpha }[/math]
und damit für die Endlage xe,ye
[math]\displaystyle{ \frac {y_e}{x_e} = \frac {g \, \sin \alpha} a }[/math]
das ist genau der doppelte Querversatz, wie er sich aus der Lösung der DGL ergibt.
Aufbauend auf diese Lösung lässt sich auch das Endergebnis aus dem Beitrag geschickter darstellen, indem man mit
[math]\displaystyle{ \dot x \equiv v_x = v_0 - a\,t }[/math]
einfach schreibt
[math]\displaystyle{ \frac a {g \sin \alpha} \,y(t) = {\frac12} v_x^2(t) \, \ln \frac{v_x(t)} {v_0} + {\frac12} a\,t\,v_x(t) + {\frac14} a\, t^2 }[/math]
Bei dieser Schreibweise ist es dann offensichtlich, dass sich im Falle vx = 0 (Endzustand) der Querversatz
[math]\displaystyle{ y_e = {\frac14} \, \frac {g \sin \alpha} a \, a\, t^2 = {\frac14} \, g \, \sin \alpha \, \left( \frac {v_0} a \right)^2 }[/math]
ergibt, wie es auch im Beitrag postuliert wird.
Details
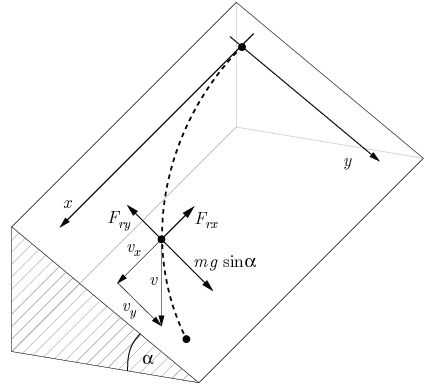
Artikel wird die mathematische Beziehung zwischen dem seitlichen Versatz d, der Geschwindigkeit v, der Fahrbahnquerneigung α, der Rutschverzögerung a, dem Bremsweg s, dem Neigungswinkel γ und der Gesamtzeit (tG) für die Vereinfachung cos γ ≈ 1 (sin γ ≈ tan γ) aufgestellt:
[math]\displaystyle{
(1a).....m \cdot \ddot x = -F_x = -F \cdot \cos \gamma
}[/math]
[math]\displaystyle{
(1b).....m \cdot \ddot y = -F_y + F_A = -F \cdot \sin\gamma + F_A
}[/math]
[math]\displaystyle{
(2a).....F = m \cdot \mu \cdot g \cdot \cos \alpha
}[/math]
[math]\displaystyle{
(2b).....F_A = m \cdot g \cdot \sin \alpha
}[/math]
[math]\displaystyle{
(2c)..... \tan \gamma = \frac {\dot y}{\dot x}
}[/math]
[math]\displaystyle{
(3).....\sin \gamma = \tan \gamma = \gamma = \frac {\dot y}{\dot x}
}[/math]
[math]\displaystyle{
(4)..... \ddot y + a \cdot \frac {\dot y}{\dot x}- g \cdot \sin \alpha = 0
}[/math]
[math]\displaystyle{
(5).....\ddot x = v_x = v_0 - a \cdot t
}[/math]
[math]\displaystyle{
(6).....\ddot y = v_y = \left(1 - \frac {a \cdot t}{v_0} \right) \cdot \left [-g \cdot \sin \alpha \cdot \frac {v_0}{a} \cdot \ln \left (1 - \frac {a \cdot t}{v_0} \right) \right]
}[/math]
[math]\displaystyle{
(7).....x = v_0 \cdot t - \frac {1}{2} \cdot a \cdot t^2
}[/math]
[math]\displaystyle{
(8).....y = g \cdot \sin \alpha \cdot \frac {v_{0}^2}{4 \cdot a^2} + g \cdot \sin \alpha \cdot \frac {v_{0}^2}{a^2} \cdot \left (1 - \frac {a \cdot t}{v_0} \right) \cdot \left [ \left (1 - \frac {a \cdot t}{v_0} \right ) \cdot \ln \left (1 - \frac {a \cdot t}{v_0} \right ) - \frac {1}{2} \right ]
}[/math]
[math]\displaystyle{
(9).....d = g \cdot \left (\frac {v}{2 \cdot a} \right)^2 \cdot \sin \alpha
}[/math]
[math]\displaystyle{
(10).....tan \gamma =\frac {g \cdot \sin \alpha}{a} \cdot ln \left ( \frac {1}{1 - \frac {t}{t_G}} \right)
}[/math]
[math]\displaystyle{
(11).....d = g \cdot \sin \alpha \cdot \frac {s}{2 \cdot a}
}[/math]
[math]\displaystyle{
(12).....a = \frac {s \cdot g \cdot \sin \alpha}{2 \cdot d}
}[/math]
Weitere Beiträge zum Thema im VuF
- 1986 #7/8 Hinweise auf die Bedeutung der Fahrbahnquerneigung in der Unfallrekonstruktion
- 1991 #4 Rutschvorgänge auf quergeneigter Fahrbahn
- 1999 #2 Deviation of the Path of a Sliding Object due to Road Camber