Zur Beurteilung der visuellen Wahrnehmbarkeit mittels digitaler Kameras
2020, p. 248 (#7/8)
Dieser Aufsatz beleuchtet die theoretischen Grundlagen sowie die praktischen Aspekte der Nachtsichtuntersuchung mittels digitaler RAW-Kameras. Auch im Jahre 2020 bezieht sich mancher Unfallanalytiker bei der Beurteilung von Dunkelheitsunfällen noch auf die Berek’schen Kurven von 1943 / 44, obwohl es spätestens seit 1969 besser aufbereitetes Datenmaterial von Adrian / Blackwell gibt, das im vorliegenden Aufsatz mit den älteren Daten verglichen wird.
On the assessment of visual perceptibility using digital cameras
This essay illuminates the theoretical basics as well as the practical aspects of night vision examination with digital RAW cameras. Even in the year 2020, some reconstructionists still refer to Berek’s curves of 1943 / 44 when assessing nighttime pedestrian accidents, although better prepared data material from Adrian / Blackwell has been available since 1969 at the latest, which is compared with the older data in this paper.
Zitat
Hugemann, W.; Zöller, H.: Zur Beurteilung der visuellen Wahrnehmbarkeit mittels digitaler Kameras. Verkehrsunfall und Fahrzeugtechnik 58 (2020), pp. 248 – 259 (#7/8)
Inhaltsangabe
Praxisfaktor bei Verwendung der Blackwell-Schwellenwerte
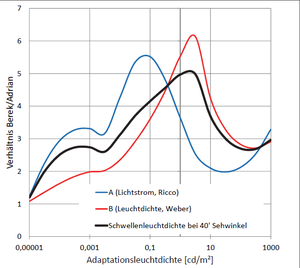
Der Beitrag macht keine konkrete Empfehlung zur Wahl des Praxisfaktors bei Verwendung der Blackwell-Adrian-Kurven. Aus dem nebenstehend abgebildeten Bild 4 des Beitrags lässt sich jedoch einfach die Empfehlung K = 4 – 5 ableiten:
Bei innerstädtisch typischen Leuchtdichten von 0,1 – 1 cd/m² beträgt das Verhältnis Berek / Blackwell 4 – 5 anstelle von Adrians globalem Anpassungsfaktor von 3,1. Letzteres entspricht dem gängigen Praxisfaktor von K = 3, der also durch K = 4 – 5 zu ersetzen ist. Höhere Praxisfaktoren sind dementsprechend bei der Verwendung der Blackwell-Schwellen mit 30 – 70 % Aufschlag zu versehen.
Verzeichnungskorrektur
In https://legacy.imagemagick.org/Usage/lens/#re-engineered wird genauer beschrieben, wie die Parameter für die Korrektur der Objektivverzeichnung anhand des RAW-Fotos und des darin eingebetteten JPEG-Thumbnails mit Excel ermittelt werden können, samt passender Excelmappe. Da diese Website leider nicht mehr gewartet wird, enthält der folgende Abschnitt die deutsche Übersetzung des dortigen Textes (der vom mir verfasst wurde.
Korrektur anhand des in das RAW-Bild eingebetteten Thumbnails
-
Rohbild (tonnenförmig verzerrt) -
Korrigiertes Vorschaubild (zum Nachbearbeiten) -
Kalibrierungspunkte -
Regressionskurve
Aktuelle Kameras (2019) bieten die Möglichkeit, die Objektivkorrektur für JPEG-Bilder intern durchzuführen. Diese Funktion wird jedoch in der Regel nicht auf RAW-Bilder angewendet. Das RAW-Bild enthält jedoch ein JPEG-Thumbnail, auf das die Korrektur bereits von der Kamera angewendet wurde. ImageMagick kann RAW-Bilder durch die Verwendung von dcraw lesen. So kann man das RAW-Bild ohne Objektivkorrektur nach JPEG konvertieren und das Ergebnis mit dem intern korrigierten JPEG-Thumbnail vergleichen. Im Falle eines solchen Bildpaares lassen sich die Korrekturparameter einfach berechnen. Durch die Auswahl entsprechender Punktpaare in beiden Bildern können wir direkt die Beziehung zwischen r und R herstellen.
Wie im obigen Beispiel (aufgenommen mit einer Sony RX100-II aus dem Jahr 2018) zu sehen ist, sind wir frei in der Wahl der Punktpaare; diese müssen weder geraden Linien folgen noch auf geometrischen Mustern liegen. Es genügt, eine Tabelle mit den entsprechenden Werten von r und R zu füllen und dann eine Regressionskurve zu berechnen, zum Beispiel mit Hilfe eines Tabellenkalkulationsdiagramms.
Die ImageMagick-Befehlszeile lautet demnach
magick barrel.jpg -distort barrel "0.0099 -0.0678 0.0014 1.0511" flat.jpg
Im obigen Beispiel ergibt die Summe der Parameter a, b, c, d nicht 1, sodass das Bild mit der Korrektur leicht vergrößert wird. Die Summe liegt jedoch nahe genug an 1, sodass wir es dabei belassen können. Standardmäßig können wir das Regressionspolynom in Excel nur dazu »zwingen«, am Ursprung (0,0) zu beginnen, können aber keine anderen Einschränkungen wie den Punkt (1,1) berücksichtigen. Diese Einschränkung kann jedoch bei Verwendung des Solver-Plugins berücksichtigt werden, wie in der Excelmapp gezeigt.
Als Alternative zur eingebauten Regressionskurve kann man die Parameter mit Hilfe der Funktion RGP berechnen, die die Parameter einer mehrdimensionalen linearen Regression bestimmt. Durch einfache Matrixmanipulationen lassen sich mit RGP die Linearkoeffizienten der Polynomnäherung berechnen. Aufgrund von numerischen Fehlern weicht das Ergebnis jedoch von der im Diagramm dargestellten Regressionskurve ab, wobei letztere präziser ist.
Als weitere Alternative können die Polynomkoeffizienten mit Hilfe von Computeralgebra-Software (CAS) wie Maxima ausgewertet werden. Dies ist genauso genau wie die Berechnung der Polynomkoeffizienten im Diagramm, lässt aber Einschränkungen zu.
Die Excelmappe und die Maxima-Datei können hier heruntergelden werden: Datei:Sony RX100M2 Tiles Distortion Parameters.zip
Korrektur anhand der im RAW-Bild eingebetteten hersteller-spezifischen Exif-Tags
Die zur Korrektur der Verzeichnung erforderlichen Daten sind bei Sony in den hersteller-spezifischen Exif-Tags hinterlegt. Diese können z.B. mit Exiftool extrahiert werden
Exiftool -t Sony
In der Ausgabe findet sich u.a. die Zeile
Distortion Corr Params 11 958 924 826 664 442 168 -148 -503 -888 -1290 -1706 0 0 0 0 0
Wie in https://stannum.io/blog/0PwljB beschrieben, handelt es sich um die Stützstellen eines Ausgleichspolynoms, das die Beziehung zwischen r und R durch die Funktionswerte an maximal 15 äquidistanten Stützpunkten beschreibt, die auf der Bilddiagonalen liegen. Die Verzeichnung wird dabei wie in PTlens als punktsymmetrisch zum Bildmittelpunkt angenommen, und beide Radien sind ebenfalls auf das Interval [0,1] normiert.
Der erste Eintrag beziffert die Anzahl der Stützpunkte, hier 11. Die folgenden Einträge αi müssen jeweils mit 214 normiert werden und ergeben dann die Radiusvergrößerung an der Stützstelle
[math]\displaystyle{ R_i = \left( 1 + \frac {\alpha_i}{2^{14}} \right) r_i }[/math]
Diese Stützstellen können mit dem Faktor D/H (Bilddiagonale zu Bildhöhe; beim 3:2-Bild etwa 1,8) auf die von PTlens verwendeten (mit der Bildhöhe bnormierten) Stützstellen umgerechnet werden und dann mit den Koeffizienten des von PTlens verwendeten Ausgleichspolynonom beschrieben werden, was in diesem Fall
magick barrel.jpg -distort barrel "0.012491447 -0.074591593 0.003717738 1.058302" Sony_flat.jpg
ergibt, also ein ähnliches Ergebnis wie bei der zuvor beschriebenen Methode.
Mit der Randbedingung a + b + c = 0 ergibt sich in Maxima
magick barrel.jpg -distort barrel "0.01224411,-0.074392235,0.003899667" Sony_flat.jpg
Die Excelmappe und die Maxima-Eingabedatei, welche die Umrechnung demonstrieren, kann hier heruntergeladen werden: Datei:Sony RX100M2 RAW Exif Distortion Parameters.zip
Lensfun-Datenbank
Mittlerweile findet sich die Sony RX100M2 auch in der lensfun-Datenbank: https://github.com/lensfun/lensfun
Dort findet sich für die kleinstmögliche Brennweite von 10,4 mm der Eintrag;
<distortion model="ptlens" focal="10.4" a="0.01545" b="-0.08481" c="0.01241"/>
was ziemlich nahe bei den nach obigen Ansätzen ermittelten Parametern liegt.
Beiträge im VuF
- 2016 #2 Lichttechnische Untersuchungen mit einer Standard-Digitalkamera
- 2020 #7/8 Zur Beurteilung der visuellen Wahrnehmbarkeit mittels digitaler Kameras
- 2023 #11/#12 Lichttechnische Untersuchung bei Fahrzeugen mit adaptiven Lichtsystemen
Literatur
Siehe auch
Eine überarbeitete englische Version des Beitrag findet sich im Tagungsband zur 32. EVU-Tagung (2024) in Kufstein.