Reifenmodell
Ein Reifenmodell (engl. BE tyre model, AE tire model) ermöglicht die Abbildung der Kräfte und Momente, die im Latsch zwischen Reifen und Fahrbahn übertragen werden mit dem Ziel der Berechnung der Fahr(zeug)dynamik. Je nach Anwendungsfall bieten sich verschiedene Modelle mit unterschiedlichem Detaillierungsgrad und entsprechender Rechenzeit an. Die Bandbreite der Anwendungen reicht von vergleichsweise einfachen mathematisch-pyhsikalischen Beschreibungen von Längs- und Querschlupf bis hin zu aufwändigen FEM-Modellen.
Beispiele für (nicht-)kommerzielle Reifenmodelle
- "Fiala-Reifenmodell"[1]
- MF-Tyre (Magic-Formula) auch Bakker-Nyborg-Pacejka Gleichungen
- IPG-Tire / TameTire[2]
- TMeasy (Tire Model easy to use)[3]
- CDTire[4]
- FTire (Flexible Structure Tire Model)[5]
- MF-Swift (Magic Formula - Short Wavelength Intermediate Frequency Tyre)[6], Erweiterung des MF-Tyre für höhere Frequenzbereiche bis 100 Hz
- RMOD-K[7]
- DTire
- HSRI (Highway Safety Research Institute, 1969; oft in ESC-Algorithmen verwendet) Link
- Hohenheimer Reifenmodell (speziell Ackerschlepper-Reifen)[8]
- Delft-Tyre, basierend auf MF-Tyre. Vertrieb durch Fa. TASS International (Helmond, NL), Link
- STI (Systems Technology Inc.) tire model, wird im NADS-Fahrsimulator verwendet
Man kann verschiedene Arten von Reifenmodellen unterscheiden: mathematische, empirische, physikalische oder Mischformen. Je nach Anwendungszweck (Fahrdynamik, Fahrkomfort) wählt man einen aufwändigeren oder einfacheren Ansatz, wobei die Rechenzeiten auch zu beachten sind. MF-Tyre ist z.B. ein Vertreter eines mathematisch-empirischen Reifenmodells.
Will man bspw. Anregungen oberhalb der Gürteleigenfrequenzen eines Reifens (ca. 30 - 50 Hz) untersuchen, um etwa ABS-Regelvorgänge (und deren Rückwirkung auf das Fahrzeug) abzubilden, so muss dieser Effekt auch im Reifenmodell enthalten sein. D.h., man wird zu einem aufwändigeren physikalischen Reifenmodell (z.B. FTire oder RMOD-K, sog. Gürtelringmodelle) greifen.
TMeasy
Beispielhaft soll das generelle Formelwerk für die Berechnung stationärer Reifenkräfte/-momente mit dem semi-physikalischen TMeasy Reifenmodell dargestellt werden. Das Reifenmodell ist in erster Linie für Handling-Anwendungen vorgesehen, d.h. die Längs- und Lateraldynamik im Reifenaufstandspunkt soll möglichst gut approximiert werden. Vorteile des Reifenmodells sind sicher die schlanke Formulierung (Rechenzeit) sowie die geringe Anzahl von notwendigen Parametern zur Beschreibung des Reifens. Für die Analyse höherfrequenter Anregungen (> ca. 8 Hz) oder einer ausgeprägten Vertikaldynamik ist das Modell jedoch nicht geeignet.
Die Radlast Fz lässt sich aus der Reifeneinfederung Δz und der zeitlichen Ableitung davon berechnen:
[math]\displaystyle{ F_z = a_1 \Delta z + a_2 (\Delta z)^2 + d_T \Delta\dot z }[/math]
Die Koeffizienten ai dienen zur Skalierung der Reifenradialsteifigkeit. Die Formel teilt sich in einen statischen (ersten) Term mit der nichtlinearen Funktion der Reifeneinfederung und einen dynamischen, geschwindigkeitsabhängigen 2. Term mit einem linearen Dämpfungselement dT. Die Radlast wird begrenzt auf Werte Fz ≥ 0.
Längs-/Umfangskraft Fx sowie Lateralkraft Fy :
Die Kräfte werden als Funktion des jeweiligen Schlupfes beschrieben, also [math]\displaystyle{ F_x = F_x (s_x) }[/math] und [math]\displaystyle{ F_y = F_y (s_y) }[/math]. Der normalisierte Längsschlupf sNx ergibt sich mit der Kontaktpunktsgeschwindigkeit vx in dieser Richtung zu
[math]\displaystyle{ s_x^N = \frac{-v_x - r_D \Omega}{r_D |\Omega|\hat s_x + v_N} }[/math],
der normalisierte Querschlupf zu
[math]\displaystyle{ s_y^N = \frac{-v_y}{r_D |\Omega|\hat s_y + v_N} }[/math].
Hierzu werden eine fiktive Grenzgeschwindigkeit vN (> 0!) eingeführt, um Singularitäten bei blockiertem Rad zu vermeiden sowie die Normalisierungsfaktoren [math]\displaystyle{ \hat s_x }[/math] und [math]\displaystyle{ \hat s_y }[/math]. Der kombinierte Schlupf s lautet dann mit Pythagoras:
[math]\displaystyle{ s = \sqrt{(s_x^N)^2 + (s_y^N)^2} }[/math].
Somit lassen sich die Kräfte Fx und Fy ausdrücken:
[math]\displaystyle{ F_x = \frac{F}{s}s_x^N }[/math], [math]\displaystyle{ F_y = \frac{F}{s}s_y^N }[/math].
Kippmoment (Tilting Torque):
Der Lateralversatz der Kraft Fz aus der Radlast bewirkt ein Kippmoment Tx. Ursache für den Versatz yQ (d.h. die Strecke zwischen geometrischem und statischem Kontaktpunkt) ist der Sturzwinkel des Reifens. Der geometrische Kontaktpunkt kann im Gegensatz zum statischen ("realen") Kontaktpunkt nach außerhalb der Kontaktfläche wandern.
[math]\displaystyle{ T_x = F_z y_Q }[/math]
Rückstellmoment (Self-Aligning Torque):
Das Reifenrückstellmoment TS wird erzeugt aus der Lateralkraft Fy mit ihrem Hebelarm des dynamischen Reifennachlaufs n (pneumatic trail oder dynamic tire offset):
[math]\displaystyle{ T_S = -n F_y }[/math]
Der Reifenachlauf wird meist als Funktion des Querschlupfes oder des kombinierten Schlupfes dargestellt. Für kleine Schräglaufwinkel lässt er sich mit der Latschlänge L abschätzen:
[math]\displaystyle{ n \thickapprox \frac {1}{6}L }[/math]
Im linearen Bereich der Seitenkraftkennlinie des Reifens wird mit zunehmendem Schräglaufwinkel auch ein größeres Rückstellmoment generiert. Mit zunehmendem Gleiten jedoch wird der Nachlauf geringer und der Kraftangriffspunkt wandert Richtung Latschmitte.
Bohrmoment (Bore Torque):
Mit dem Bohrschlupf
[math]\displaystyle{ s_B = \frac {-R_B \omega_n}{r_D |\Omega|+v_N} }[/math]
ergibt sich das Bohrmoment TB zu
[math]\displaystyle{ T_B = R_B F(s_B) }[/math]
RB stellt den äquivalenten Bohrradius dar, der bei 2/3 des Radius der durch eine Kreisfläche approximierten Latschfläche liegt. Mit dem Bohrschlupf sB kann man nun einen dreidimensionalen Schlupf sG beschreiben:
[math]\displaystyle{ s_G = \sqrt{s^2 + s_B^2} }[/math]
Mit dieser Schlupfformulierung ließe sich das Bohrmoment nochmals verfeinert beschreiben, da bei einer Bohrbewegung nicht nur der Bohrschlupf separat, sondern in Kombination mit Längs- und Querschlupf wirksam ist.
Bohrmoment und Rückstellmoment lassen sich als Moment um die z-Achse zusammenfassen zu
[math]\displaystyle{ T_z = T_S + T_B }[/math]
Das Rollwiderstandsmoment TY ist für fahrdynamische Betrachtungen eher unerheblich, soll aber trotzdem kurz erwähnt werden, da es im TMeasy-Modell berücksichtigt wird. TY ergibt sich aus der Radaufstandskraft Fz mit dem Hebelarm xRW. Der Hebelarm entsteht beim rollenden Rad dadurch, dass Fz nicht radmittig angreift, sondern sich im Latsch druckbedingt nach vorne verschiebt.
[math]\displaystyle{ T_Y = F_z x_{RW} }[/math]
Der Hebelarm xRW kann aus dem Produkt von Rollwiderstandsbeiwert fR und Reifenradius r0 berechnet werden.
Hinweis:
- Die Implementierung in PC-Crash ist demgegenüber vereinfacht!
- Im Fahrzeugdynamik-Skript von Prof. Rill (siehe unten) findet sich in Kapitel 7.4.1 ein Parametersatz (insgesamt 46 Parameter) für ein TMeasy-Reifenmodell. Im Vergleich dazu nachfolgend ein Auszug (!) aus einem Parametersatz eines MF-tyre Reifenmodells. Für die Abbildung des Lateralverhaltens werden 34 Parameter benötigt.
Verwendung von Reifenmodellen in Unfallrekonstruktionsprogrammen
1. Virtual Crash
Hier (bis Software-Version 2.2) lässt sich je Reifen ein maximaler Schräglaufwinkel in Grad eingeben (möglicher Wertebereich: 0,01° – 50°). Standardmäßig ist der Winkel auf 10° eingestellt. Auch wenn keine Dokumentation hierzu vorhanden ist, ist anzunehmen, dass die Lateralkraft linear bis hin zum maximalen Schräglaufwinkel aufgebaut wird.
Bei VCrash 3 lassen sich bspw. unter Eigenschaften des betreffenden Fahrzeugs unter Achsen für Achse 1 und 2 folgende Reifenmodelle (wahlweise auch Reifen unterschiedlich) einstellen:
- "Konstante"
- "Linear"
- "TMeasy"
Die beiden letztgenannten Modelle können nach Anwahl dann in einer Diagrammdarstellung verändert werden: Im linearen Modell kann der max. Schräglaufwinkel (Defaultwert: 10°) von 0,01° – 85° vorgegeben werden. Im TMeasy-Modell können Quer- und Längskomponenten des Reifenmodells editiert werden.
2. Analyzer Pro
Die Software verwendet das IPG-Tire Modell (mittlerweile weiterentwickelt und TameTire genannt) der Fa. IPG Automotive aus Karlsruhe.
3. PC-Crash
Die Software PC-Crash bietet 2 Reifenmodelle zur Auswahl an:
- Lineares Reifenmodell: Vorgabe des maximalen Schräglaufwinkels pro Reifen (defaultmäßig 10°)
- TMeasy Reifenmodell: freie Vorgabe der Lateral- und Longitudinalparameter pro Reifen
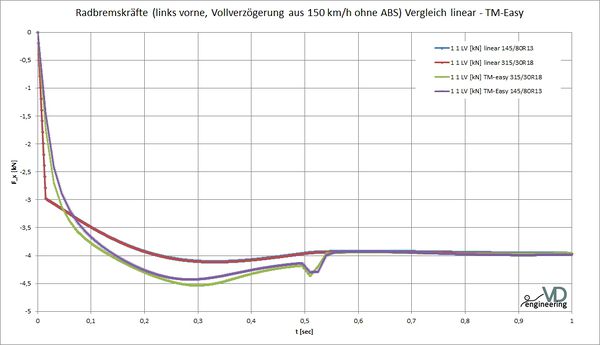
Im Kontext des Reifenmodells ist auch noch die Eingabe einer Reifengröße und -breite möglich. Während diese Angaben beim linearen Modell nicht in die Berechnung der Reifenkräfte einfließen, sondern der Visualisierung (2D/3D) dienen, fließt im TM-Easy Reifenmodell der durch Nutzereingabe der Reifendimension errechnete Raddurchmesser sehr wohl in die Berechnung der Radkräfte ein. Nachfolgendes Diagramm zeigt die Unterschiede bei einer Vollverzögerung zwischen linearem und TMeasy Modell sowie 2 exemplarischen Reifendimensionen (145 / 80 R 13 mit Durchmesser 562 mm und 315 / 30 R 18 mit 646 mm), wobei nur der Beginn der Bremsung dargestellt ist.
Ein Grund für den unterschiedlichen Bremskraftaufbau beim TMeasy Modell dürfte sein, dass in der Definition des Längsschlupfes der dynamische Rollradius auftaucht, in dessen näherungsweise Berechnung der unbelastete Reifenradius einfließt.
4. Sonstiges
Ein direkter Vergleich der Reifenmodelle zwischen PC-Crash und Virtual Crash scheitert daran, dass Virtual Crash weder in Version 2.x noch in 3.0 Reifenkräfte ausgibt bzw. dem Anwender zugänglich macht.
Parametrisierung
- Schräglaufwinkel
- Hier scheiden sich wohl die Geister. Während PC-Crash dem Nutzer des linearen Modells einen maximalen Winkel von 10° empfiehlt, wird im Buch Fahrzeugreifen und Fahrwerkentwicklung (1. Auflage 2009) ein Maximum der Schräglaufsteifigkeit bei ca. 3,5 - 4,5 Grad Schräglaufwinkel angegeben. Das würde sich mit der Empfehlung aus Simulation of Vehicle Accidents using PC-Crash (S. 21) etwa decken. Der Dubbel geht von 5 - 15° aus. Im Buch Vehicle Dynamics kann man ein Maximum zwischen 6 und 8° nachlesen. Alle genannten Zahlenwerte beziehen sich auf Straßenreifen (Serien- und keine Rennreifen). Da der Seitenkraft-Schrägwinkel-Verlauf von einer Vielzahl von Parametern (Reifeninnendruck, Radlast, Abnutzungsgrad, Alter, Fahrgeschwindigkeit, Radsturz usw.) abhängig ist, die der Rekonstrukteur nicht kennen wird und ein vermessenes Reifenkennfeld für den verwendeten Reifen auch so gut wie nie zur Verfügung steht, lässt sich im Zweifel kein Wert zwischen 3 und 15° kategorisch ausschließen.
- Es ist nochmals darauf hinzuweisen, dass es sich bei dem diskutierten Wert nicht um den im "normalen" Fahrbetrieb auftretenden maximalen Schräglaufwinkel (meist < 12°; Fahrwerkhandbuch) dreht, sondern um den Wert, bei dem bzw. ab dem die maximale Seitenführungskraft aufgebaut wird.
- TMeasy Reifenmodell
- Ein ausführlich vermessener Nutzfahrzeugreifen der Größe 11 R 22,5 samt Kennfeldern findet sich im Kraftfahrtechnischen Taschenbuch 26. Auflage, dort S. 802 ff.
- In Simulation of Vehicle Accidents using PC-Crash, S. 194 f sind Parametrierungsdaten eines auf dem Prüfstand vermessenen Reifen der Dimension 315/80 R 22,5 aufgeführt.
- In [1], S. 5 sind gemessene Längs- und Querkraftkennlinien für einen Pkw-Reifen 225/60 R 16 bei verschiedenen Radlasten gezeigt.
- Bei Pacejka, Tyre and Vehicle Dynamics (2. Auflage, S. 210 f), sind die vermessenen Kraftcharakteristiken eines Pkw-Reifen (195/65 R15) sowie eines Lkw-Reifen (315/80 R22,5) zu finden. Allerdings sind die Kennlinien (jeweils 3 versch. Radlasten) noch nicht normiert, so dass für eine Eingabe ins TMeasy Reifenmodell noch etwas Umrechnungsarbeit erforderlich ist.
- Defaultbedatung in PC-Crash: Fmax = 1.1; Smax = 0.21; Fgleit = 1; Sgleit = 0.5; F0p = 15; I = 2 kgm2;
- aus Kiefer, A.; Bilek, D.; Moser, A.; Webb, A.: A Comparison Study between PC-Crash Simulation and Instrumented Handling Maneuvers. SAE:2011-01-1121, 2011: Reifen: Firestone Wilderness AT P235/75R15 (1999 Ford Explorer)
- voll beladen: Fmax = 0.906; Smax = 0.17; Fgleit = 0.94; Sgleit = 0.377; F0p = 9.5; I = 2 kgm2;
- leicht beladen: Fmax = 1.01; Smax = 0.21; Fgleit = 0.99; Sgleit = 0.55; F0p = 15; I = 2 kgm2;
- Longitudinal- und Lateralparameter sind identisch parametriert.
Reifen-Kennfelder
Pkw
Nfz
- Michelin XZA 12 R 22.5 - Von Glasner, E. C.: Steigerung der aktiven Sicherheit von Nutzfahrzeugen mit Hilfe der fahrdynamischen Simulation. Habilitation 1987.
Zweirad
Kommentar
--Vdengineering (Diskussion) 00:28, 4. Jan. 2015 (CET)
Auch wenn in S. 84 Handbuch Verkehrsunfallrekonstruktion, 2. Auflage das TMeasy Modell so beschrieben wird, dass "der Sturzeinfluss durch Einführung eines modifizierten Querschlupfes berücksichtigt" wird, so ist nicht ganz klar, ob das auch so in PC-Crash implementiert ist. Denn dann müssten sich - wenn auch keine betragsmäßig großen - Seitenführungskräfte am Reifen auch bereits bei 0° Schräglaufwinkel (Geradeausfahrt) aufbauen.
Lt. Simulation of Vehicle Accidents using PC-Crash S.22 wurde in PC-Crash das ursprüngliche TMeasy Reifenmodell vereinfacht, es werden "nur" die Längs- sowie die Querkraftcharakteristiken berücksichtigt. Rückstellmomente, Bohrmomente, Rollwiderstände sowie auch Sturzeinflüsse werden damit vernachlässigt.
Weitere Beiträge zum Thema im VuF
Literatur
- Rill, G.: Simulation von Kraftfahrzeugen, Regensburg, 1994, Nachdruck
- Pacejka, H.B.: Tyre and Vehicle Dynamics, Butterworth-Heinemann Oxford, Second Edition 2006
- Gnadler, R.; Frey, M.; Unrau, H.-J.: Kraftschluss- und Verformungsverhalten von Fahrzeugreifen bei extremen Fahrmanövern, ATZ 10/2006, siehe auch FAT-Schriftenreihe Nr. 192
- Brach, R.; Brach, M.: Über die in Unfallsimulationsprogrammen verwendeten Reifenmodelle, Proceedings of the 17th EVU Conference, Nice 2008, pp. 271 - 290
- Schramm, D. et. al.: Modellbildung und Simulation der Dynamik von Kraftfahrzeugen, 2. Auflage 2013
- Ammon, D.; Gnadler, R.; Mäckle, G.; Unrau, H.-J.: Ermittlung der Reibwerte von Gummistollen zur genauen Parametrierung von Reifenmodellen, ATZ 2004 Heft 7/8 S. 694 ff
- SIMPACK News, March 2014
SAE Papers
Liste ohne Anspruch auf Vollständigkeit!
- Dodge, R.: The Dynamic Stiffness of a Pneumatic Tire Model. SAE Technical Paper SAE:650491, 1965
- Bakker, E.; Pacejka, H.; Lidner, L.: A New Tire Model with an Application in Vehicle Dynamics Studies. SAE Technical Paper SAE:890087, 1989
- Allen, R.; Magdaleno, R.; Rosenthal, T.; Klyde, D. et al.: Tire Modeling Requirements for Vehicle Dynamics Simulation. SAE Technical Paper SAE:950312, 1995
- Gim, G.; Kang, N.: Requirements of a Tire Model for Practical Cornering Simulations of Vehicles. SAE Technical Paper SAE:960179, 1996
- Allen, R.; Rosenthal, T.; Chrstos, J.: A Vehicle Dynamics Tire Model for Both Pavement and Off-Road Conditions. SAE Technical Paper SAE:970559, 1997
- Allen, R.; Rosenthal, T.; Klyde, D.; Chrstos, J.: Vehicle and Tire Modeling for Dynamic Analysis and Real-Time Simulation. SAE Technical Paper SAE:2000-01-1620, 2000
- Allen, R.; Myers, T.; Rosenthal, T.; Klyde, D.: The Effect of Tire Characteristics on Vehicle Handling and Stability. SAE Technical Paper SAE:2000-01-0698, 2000
- Liu, Q.; Solis, D.; Pan, W.: Analysis of the STI Tire Model. SAE Technical Paper SAE:2002-01-1579, 2002
- Salaani, M.: Analytical Tire Forces and Moments Model With Validated Data. SAE Technical Paper SAE:2007-01-0816, 2007
- Brach, R.; Brach, M.: Tire Models for Vehicle Dynamic Simulation and Accident Reconstruction. SAE Technical Paper SAE:2009-01-0102, 2009
Siehe auch
- Wikipedia - Reifenmodell
- www.autogumi.com/FDV_Skript.pdf Skriptum Fahrzeugdynamik FH Regensburg Prof. G. Rill, 2001
- Literaturliste: Fahrdynamik
- Tesis DYNAware Simulationssoftware
Einzelnachweise
- ↑ Fiala, E.: Seitenkräfte am rollenden Luftreifen. Dissertation an der TU Wien, 1954
- ↑ http://ipg.de/de/simulationsolutions/tametire/
- ↑ http://tmeasy.de/
- ↑ http://www.itwm.fraunhofer.de/abteilungen/mdf/leistungen-und-produkte/cdtire.html
- ↑ https://www.cosin.eu/
- ↑ https://www.tassinternational.com/delft-tyre-mf-tyremf-swift
- ↑ http://www.rmod-k.com/
- ↑ https://reifenmodell.uni-hohenheim.de/