Eine grafisch/mathematische Methode zur Auswertung von Lichtbildern
1987, p. 36 (#2)
Es wird ein Verfahren zur Entzerrung von Lichtbildern vorgestellt. Durch Kombination von grafischen und mathematischen Methoden wird ein Raster erzeugt, so daß die Bildinformation maschenweise in eine maßstäbliche Skizze übertragen werden kann.
A process is herewith presented for correcting distortions in photographs. By combining graphical and mathematical methods, a grid is created which enables the information on the photograph to be transferred mesh-wise onto a scale drawing.
Zitat
Becke, M.; Hebing, N.: Eine grafisch/mathematische Methode zur Auswertung von Lichtbildern. Verkehrsunfall und Fahrzeugtechnik 25 (1987), pp. 36 – 38 (# 2).
Inhaltsangabe
Die Veröffentlichung greift die bereits im Jahr zuvor angestellten Überlegungen betreffend die projektive Abbildung von Geraden auf. Die ungewöhnliche Art der Darstellung, in der die Bildebene (wie in der Kamera) hinter dem Projektionszentrum liegt, deutet darauf, dass es sich um weitgehend eigenständige Überlegungen der Autoren handelt.
Letztlich geht es darum, wie man auf einer gegebenen Geraden einen Abstand ermittelt, wenn zwei Abstandsmaße auf derselben Geraden bekannt sind. In der Veröffentlichung wird dies dazu benutzt, das Foto mit einem definierten Möbiusnetz zu überziehen - was nur eine der denkbaren Anwendungen ist.
Die Darstellung der Herleitung ist stark verkürzt und Nomenklatur wie Bezugspunkte teilweise ungeschickt gewählt, sodass die Veröffentlichung unnötig schwer verständlich ist. Die nachstehende Erläuterung soll diesbezüglich Abhilfe schaffen, denn die Überlegungen sind im Einzelfall heute immer noch brauchbar, etwa wenn die vollständige Vierpunkt-Kalibrierung infolge fehlender Maße nicht gelingt.
Ergänzende Erläuterung
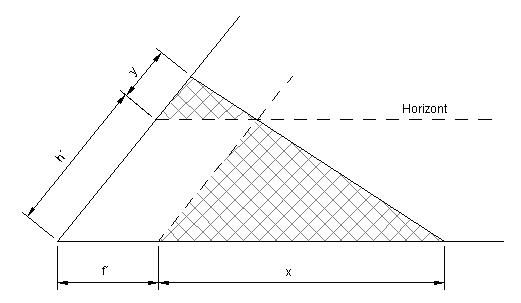
Die Herleitung der Formeln ist etwas kompliziert dargestellt. Die unten stehende Abbildung ist etwas einfacher als ihr Pendant in der Veröffentlichung.
Wegen der Ähnlichkeit der grau schraffierten Dreiecke ergibt sich: [math]\displaystyle{ \frac {x}{h'} = \frac {f'}{y} }[/math]
und daraus: [math]\displaystyle{ x \cdot y = h' \cdot f' }[/math]
Die Bezeichnungen h' und f' deuten dabei (anders als die in der Veröffentlichung gewählten Bezeichnungen) an, dass diese Größen mit der Aufnahmehöhe h über Grund und der (virtuellen) Brennweite f (focal length) in enger Beziehung stehen. Wir wählen drei willkürliche Punkte (x0,y0), (x1,y1) und (x2,y2). Dann gilt: [math]\displaystyle{ x_1 \cdot y_1 = x_0 \cdot y_0 \\ x_2 \cdot y_2 = x_0 \cdot y_0 }[/math]
Im Bild lassen sich die Abstände y0, y1 und y2 vom Horizont im Regelfall direkt ausmessen, weil die Horizontlinie meist aus dem Fluchtpunkt der Fahrbahn ermittelt werden kann. Die Abstände x0, x1 und x2 lassen sich hingegen nicht direkt messen, weil die Fußgerade der Bildebene auf der Fahrbahnebene nicht bekannt ist. Dort lassen sich nur die Differenzen: [math]\displaystyle{ \Delta x_1 \,= (x_1 - x_0) \\ \Delta x_2 \,= (x_2 - x_0) }[/math]
ausmessen, die unabhängig vom Ursprung des Koordinatensystems sind. Sicherheitshalber führt man solche Relativkoordinaten auch im Bild ein. Dort gilt analog: [math]\displaystyle{ \Delta y_1 \,= (y_1 - y_0)\\ \Delta y_2 \,= (y_2 - y_0) }[/math]
Einsetzen ergibt: [math]\displaystyle{ (x_0 + \Delta x_1) \cdot (y_0 + \Delta y_1) = x_0 \cdot y_0\\ (x_0 + \Delta x_2) \cdot (y_0 + \Delta y_2) = x_0 \cdot y_0 }[/math]
oder auch:
[math]\displaystyle{ \Delta y_1 \cdot x_0 + \Delta x_1 \cdot y_0 + \Delta x_1 \cdot \Delta y_1 = 0 \\ \Delta y_2 \cdot x_0 + \Delta x_2 \cdot y_0 + \Delta x_2 \cdot \Delta y_2 = 0 }[/math]
Es ergibt sich also ein lineares Gleichungssystem für die Unbekannten x0 und y0. Die Lösung lautet: [math]\displaystyle{ x_0 = \frac {\Delta x_1 \Delta x_2 \cdot (\Delta y_2 - \Delta y_1)} {\Delta x_1 \Delta y_2 - \Delta y_1 \Delta x_2}\\ y_0 = \frac {\Delta y_1 \Delta y_2 \cdot (\Delta x_2 - \Delta x_1)} {\Delta x_1 \Delta y_2 - \Delta y_1 \Delta x_2} }[/math]
Das sind die Beziehungen aus der Veröffentlichung – in etwas anderer Nomenklatur. Nachdem jetzt x0 und y0 bekannt sind, kann eine beliebige Bildkoordinate y (oder auch Δy) in die wirkliche Koordinate umgerechnet werden und umgekehrt.
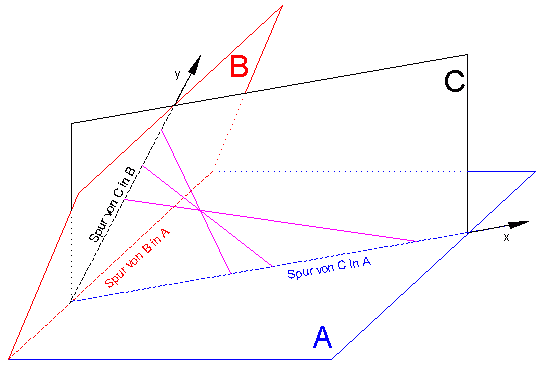
Abb. 1 aus der Veröffentlichung ist bezüglich der Lage der Ebene C etwas unklar. Die nachfolgende, farbige Abbildung macht deutlich, was gemeint ist:
Abb. 2 liegt in der Ebene C, die annähernd senkrecht auf der Fahrbahn steht und in eine bestimmte Richtung weist – nicht notwendigerweise in Blickrichtung der Kamera! Die über die drei Punkte hergeleiteten Beziehungen gelten nur in dieser Ebene C, also auf einer ganz bestimmten Linie und nicht etwa allgemein im Bild!
Weitere Beiträge zum Thema im VuF
- 1986 #10 Spurensicherung - grafische Fotoauswertung mit der Rasterfeldmethode -
- 1987 #2 Eine grafisch/mathematische Methode zur Auswertung von Lichtbildern
- 1997 #6 Direkte fotogrammetrische Verkehrsunfallanalyse
- 2004 #5 Versuche zur fotogrammetrischen Auswertung von Geschwindigkeits-Messfotos
Weitere Beiträge zum Thema
- Brennweiten der Schneider-Objektive
- Brennweiten der Nikor-Objektive
- Robot SmartCamera
- Literaturliste: Verkehrsmesstechnik
- Nachstellen der Kameraperspektive in PC-Crash
Weitere Infos zum Thema
allgemeine Literatur zum räumlichen Zeichnen