Auswertung der Leuchtspuren in Messfotos

Aus Colliseum
Zur Navigation springen Zur Suche springen

Zitat

Hugemann, W.: Auswertung der Leuchtspuren in Messfotos. Colliseum 2012

Problemstellung

Leuchtspuren bei einer Rechtsmessung mit PoliScan Speed

Auf Digitalfotos, die bei Geschwindigkeitsmessungen zur Beweissicherung geschossen werden, sind oft dünne Leuchtspuren zu erkennen, die – ausgehend von hellen Punkten am Fahrzeug, oft den Scheinwerfern – schräg nach unten übers Foto laufen. Diese Spuren kann man dazu nutzen, die Geschwindigkeit des fotografierten Fahrzeugs zu bestimmen. Damit lässt sich das Messergebnis unabhängig von der eigentlichen Messung (mittels Radar, Lidar oder Einseitensensor) überprüfen.

Der Effekt beruht auf den technischen Besonderheiten der in den CMOS-Kameras eingesetzten Interline Transfer CCDs: Solche Kameras arbeiten (aus Kostengründen) mit einem rein elektronischen Verschluss: Bei der Belichtung werden die Chipladungen im ersten Schritt in abgedunkelte Spalten zwischen den fotoaktiven Spalten des Chips verschoben. In diesen abgedunkelten Spalten werden sie anschließen »nach unten« abtransportiert, wobei die »unten« herausfließenden Ladungen über einen AD-Wandler gemessen werden. Der Ladungsgehalt einer Zelle ist dann das Maß für die Helligkeit des entsprechenden Bildpunkts.

Aufgrund von Beugungseffekten dringt das Licht besonders heller Objekte seitlich in die abgedunkelten Spalten ein und erhöht nach Ende der »offiziellen« Belichtung den Ladungsgehalt der abtransportierten Zellen. Über diesen Effekt hinterlassen helle statische Objekte vertikale Linien auf dem Foto. Bewegt sich das Leuchtobjekt (teilweise) in horizontaler Richtung, entsteht diese Zusatzbelichtung in den einzelnen Sensorspalten zu unterschiedlichen Zeitpunkten, nämlich dann, wenn die Lichtquelle die jeweilige Spalte erreicht hat. Die Leuchtspur verläuft dann schräg über das Bild; die Horizontalgeschwindigkeit bestimmt den Winkel gegenüber der Vertikalen.

Bereits im Wartezustand das CCD-Sensors, vor der elektronischen Belichtung, müssen die Ladungen in gleicher Weise ständig abtransportiert werden, damit die fotoaktiven Zellen nicht »überlaufen«. Die Leuchtspuren entstehen deshalb nicht erst nach der Belichtung, sondern schon im Zeitraum davor. Allerdings ist der Abtransport der Ladungen vor der Belichtung oft schneller, da die Ladungswerte der Zellen nicht über den AD-Wandler ausgewertet werden müssen. Dieser schnellere Abtransport vor der Belichtung macht sich in einem »Spurknick« bemerkbar; die Spuren verlaufen vor der Belichtung steiler. In manchen CCD-Kameras, so etwa der Jenoptic SmartCamera, ist der Ladungstransport vor und nach der Belichtung gleich schnell. Die Leuchtspuren verlaufen in diesem Fall glatt durch den Leuchtpunkt hindurch.

Der Lidar-Spezialist Vitronic verbreitet die unten zitierte Schrift, in der die Auswertung detailliert beschrieben wird. Diese Ausarbeitung wurde jedoch offenbar nicht unter didaktischen Gesichtspunkten verfasst und ist daher unnötig schwer verständlich. Der vorliegende Artikel bemüht sich daher, den Rechengang nachvollziehbarer zu erläutern und dabei eine schlüssigere Nomenklatur zu verwenden.

Grundgedanke

Aufnahmesituation

Im Winkel, den die Leuchtspuren mit der Vertikalen einschließen, verbirgt sich das Verhältnis von vertikaler Auslesegeschwindigkeit des CCD-Chips und der Horizontalgeschwindigkeit des Leuchtpunkts auf dem Chip. Diese wiederum lässt sich über den Abstand [math]\displaystyle{ R }[/math] des Fahrzeugs zur Kamera und deren Winkel [math]\displaystyle{ \psi }[/math] der Kamera zur Fahrbahn (genauer: zur Bewegungsrichtung des fotografierten Fahrzeugs) in die Geschwindigkeit [math]\displaystyle{ v }[/math] des Fahrzeugs umrechnen.

Der Abstand [math]\displaystyle{ R }[/math] des Fahrzeugs zur Kamera bei Auslösung des Fotos ergibt sich, indem über die Größe (meist: die Breite) [math]\displaystyle{ b }[/math] eines Objekts im Bild und seine tatsächliche Größe [math]\displaystyle{ B }[/math] umrechnet. Dazu wird die Brennweite [math]\displaystyle{ f }[/math] des Objektivs benötigt. Für diese Abstandsbestimmung bietet sich etwa das Kennzeichen an, das in der Regel bei Pkw 50 cm breit ist; man kann jedoch auch ein fahrzeugspezifisches (am besten größeres) Maß verwenden, wie etwa den Abstand der linken und rechten Hauptscheinwerfer. An dieser Stelle ist auch auf Bladt's Veröffentlichung hinzuweisen. Dort wird vorgeschlagen, die etwas geringere Breite (46,6 cm) des weißen Bereichs des mit genormten Größen versehenen EURO-Kennzeichens sowie die Ziffernhöhe (7,5 cm) zur Auswertung heranzuziehen.

Die Herleitung geht davon aus, dass sich die Objekte, welche die Leuchtspuren zeichnen, bei der Annäherung genau waagerecht auf dem Bildhorizont bewegen. Das ist in der Praxis nur näherungsweise der Fall, weil die Frontscheinwerfer unterhalb der Objektivhöhe liegen. Außerdem setzt die Herleitung den Winkel [math]\displaystyle{ \psi }[/math] gegenüber der Fahrbahn als bekannt voraus, was so einfach nur bei stationären Anlagen der Fall ist.

Die Brennweite [math]\displaystyle{ f }[/math] der eingesetzten Kamera kann man meist dem Messprotokoll entnehmen. Werden (wie bei Vitronic PoliScanSpeed) zwei Kameras verwendet, so ist die Kamera in den Zusatzdaten im Messcontainer protokolliert (Vitronic: cam0, cam1). Liegen alle Fotos der Messserie vor, ergibt sich diese Information auch aus dem Bildinhalt selbst, indem man mit den übrigen Fotos vergleicht.

Für die Berechnung der Geschwindigkeit [math]\displaystyle{ V }[/math] des Fahrzeugs werden also drei Bausteine benötigt:

  • Horizontalgeschwindigkeit des Leuchtpunkts auf dem CCD-Chip (anhand des Winkels)
  • Abstand des Fahrzeugs von der Kamera (aus der Bildgröße eines bekannten Objekts)
  • Eventuell: Winkel der Leuchtquelle zur der Objektivachse

Berechnung

In der nachfolgenden Berechnung wird die Nomenklatur des Originalskripts vereinfacht:

  • Größen in der realen Welt (etwa die Breite des Kennzeichens [math]\displaystyle{ B }[/math]) werden mit Großbuchstaben bezeichnet, die Größe deren Bildes mit dem gleichlautenden Kleinbuchstaben (also [math]\displaystyle{ b }[/math] beim Bild des Kennzeichens).
  • Im Originalmanuskript wird bei allen Bildgrößen noch ein Skalierungsfaktor [math]\displaystyle{ s_y }[/math] eingefügt um von der Bildgröße in Pixel auf eine absolute Größe (in mm, wie bei der Brennweite) zu gelangen. Wir verzichten im Folgenden auf diesen Faktor, indem wir davon ausgehen, dass entweder die Bildgröße [math]\displaystyle{ b }[/math] in mm oder aber die Brennweite [math]\displaystyle{ f }[/math] in Pixel angegeben ist.

Fahrzeugabstand und -geschwindigkeit

Der Fahrzeugabstand [math]\displaystyle{ R }[/math] ergibt sich aus der realen Objektgröße [math]\displaystyle{ B }[/math], dessen Bildgröße [math]\displaystyle{ b }[/math] und der Brennweite [math]\displaystyle{ f }[/math]. Dabei ist zu berücksichtigen, dass die Fahrzeugfront von der Kamera unter dem Winkel [math]\displaystyle{ \psi }[/math] gesehen wird, was die scheinbare Breite des Objekts auf [math]\displaystyle{ B \cos \psi }[/math] verkleinert: [math]\displaystyle{ \frac {B \cos \psi} R = \frac b f }[/math]

Die Umrechnung zwischen der Geschwindigkeit [math]\displaystyle{ V }[/math] einer Leuchtquelle und der Horizontalgeschwindigkeit [math]\displaystyle{ v_x }[/math] des Leuchtpunktes im Bild läuft völlig analog: [math]\displaystyle{ \frac {V \sin \varphi'} {R'} = \frac {v_x} f }[/math] Der beliebig gewählte Leuchtpunkt hat dabei einen die leicht abweichende Orientierung [math]\displaystyle{ \varphi' }[/math] zur Kamera und einen etwas anderen Abstand [math]\displaystyle{ R' }[/math] zur Kamera als der Abstand [math]\displaystyle{ R }[/math] der Kennzeichenmitte. In der Formel erscheint nun der Sinus anstelle des Kosinus, da die Fahrzeuggeschwindigkeit senkrecht auf der Fahrzeugfront steht.

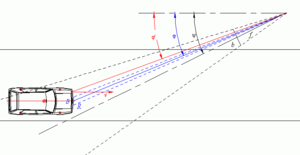
Wir gehen vereinfachend davon aus, dass die Frontkontur kastenförmig ist, sodass die Frontkontur in der Draufsicht eine gerade Linie bildet, so wie z.B. beim VW Golf II, der in der Illustration auf dieser Seite verwendet wird. Dann haben Leuchtpunkt und Kennzeichenmitte in Längsrichtung der Straße denselben Abstand zur Kamera, sodass gilt: [math]\displaystyle{ R' \cos \varphi' = R \cos \varphi }[/math]

Horizontalgeschwindigkeit auf dem Chip

Die Leuchtspur schließt den Winkel [math]\displaystyle{ \alpha }[/math] mit der Vertikalen ein, sodass gilt: [math]\displaystyle{ \tan \alpha = \frac {v_x}{v_y} }[/math] Die Vertikalgeschwindigkeit wird typischerweise durch ihren Kehrwert, die Zeilenauslesezeit [math]\displaystyle{ \tau }[/math] beschrieben. Diese beträgt bei der im Poliscan-Speed eingesetzten Kamera 112 µs, was einer Vertikalgeschwindigkeit von 8928,5 px/s entspricht. Es gilt also: [math]\displaystyle{ v_x = \frac {\tan \alpha} {\tau} }[/math]

Fahrzeuggeschwindigkeit

Indem man die bisherigen Beziehungen nacheinander einsetzt, ergibt sich: [math]\displaystyle{ V = \frac {R'} {\sin \varphi'} \frac {v_x} f = \frac {R \cos \varphi} {\cos \varphi' \sin \varphi'} \frac {\tan \alpha} {\tau f} =\frac {B \cos\psi \cos \varphi} {b \cos \varphi' \sin \varphi'} \frac {\tan \alpha} \tau }[/math] und mit: [math]\displaystyle{ \sin 2 \varphi' = 2 \cos \varphi' \sin \varphi' }[/math] dann die Gleichung, die (in komplizierterer Schreibweise) auch im Vitronic-Skript steht: [math]\displaystyle{ V = \frac {2 B \cos\psi \cos \varphi} {b \sin 2\varphi'} \frac {\tan \alpha} \tau }[/math]

Fehlende Winkel

Der Winkel [math]\displaystyle{ \varphi }[/math] lässt sich aus dem Blickwinkel der Kamera [math]\displaystyle{ \psi }[/math] und dem Horizontabstand [math]\displaystyle{ x }[/math] des Bildpunktes von der Bildmitte berechnen: [math]\displaystyle{ \varphi = \psi \pm \arctan \frac x f }[/math] und analog dazu der Winkel [math]\displaystyle{ \varphi' }[/math] sowie jeder andere entsprechende Winkel. Das Vorzeichen ± ist je nach Fahrtrichtung des Fahrzeugs im Foto zu wählen: Fährt es von links nach rechts (sog. Linksmessung, weil der linke Fahrbahnrand [in Blickrichtung der Kamera] näher liegt), so wächst der Winkel, je weiter man im Foto nach rechts geht, und es gilt das positive Vorzeichen. Fährt das Fahrzeug von rechts nach links (sog. Rechtsmessung), so gilt das Minuszeichen.

Die Umrechnung auf den tatsächlichen Winkel [math]\displaystyle{ \varphi' }[/math] ist relativ einfach und auch relativ wichtig. Würde man darauf verzichten und alle Winkel mit der Orientierung [math]\displaystyle{ \psi }[/math] der Kamera gleichsetzen, so wäre dies für die Kennzeichenmitte leicht zu vertreten, denn diese befindet sich nahezu in der Bildmitte, sodass [math]\displaystyle{ \varphi \approx \psi }[/math]. setzt man die gleiche Approximation für den Winkel [math]\displaystyle{ \varphi' }[/math] an, so beträgt der relative Fehler: [math]\displaystyle{ \frac{\sin \varphi' \, \cos \varphi'}{\sin \psi \, \cos \psi} - 1 = \frac{\sin (\psi + \Delta) \, \cos (\psi + \Delta)}{\sin \psi \, \cos \psi} - 1 }[/math] Die Abweichung [math]\displaystyle{ \Delta }[/math] entspricht etwa der halben Breite der Front, die wiederum typischerweise etwa auf einem Drittel der Bildbreite abgelichtet ist. Damit beträgt [math]\displaystyle{ \Delta }[/math] etwa ein Sechstel des horizontalen Objektivöffnungswinkels (HFOV = horizontal field of view, siehe weiter unten). Wenn der Kamerawinkel gegenüber der Fahrbahn etwa 20° beträgt, macht die Korrektur damit schnell ca. 10° aus.

Kameraorientierung

Für die Berechnungen muss der Blickwinkel [math]\displaystyle{ \psi }[/math] der Kamera zu Fahrbahn bekannt sein. Dies ist aber a priori nur bei fest installierten Anlagen der Fall. Bei Messungen aus dem Fahrzeug oder von einem Stativ muss der Winkel hingegen aus dem Bildinhalt berechnet werden. Dazu lässt sich etwa der Abstand des Fluchtpunkts [math]\displaystyle{ x_{0f} }[/math] der Fahrbahn von der Bildmitte verwenden, denn es gilt: [math]\displaystyle{ \tan \psi = \frac {x_{0f}} f }[/math] Kann der Fluchtpunkt der Fahrbahn nicht (verlässlich) ermittelt werden, weil nicht genug Hilfslinien konstruiert werden können, kann man ersatzweise auf die Eckpunkte der Auswerteschablone zurückgreifen. Wenn diese perspektivisch korrekt ins Bild eingeblendet ist, steht sie senkrecht zur Fahrbahn (bzw. quer zur Fahrtrichtung des Pkw), sodass der Abstand ihres Fluchtpunkts [math]\displaystyle{ x_{0s} }[/math] mit demjenigen der Fahrbahn über: [math]\displaystyle{ x_{0f} \, x_{0s} = f^2 }[/math] verknüpft ist. Mithin ist: [math]\displaystyle{ \tan \psi = \frac {x_{0f}} f = \frac {f^2} {f x_{0s}} = \frac f {x_{0s}} }[/math] Die Koordinaten der Eckpunkte der Auswerteschablone kann man auf die gleiche Weise bestimmen wie diejenigen eines jeden anderen Punktes. Alternativ kann man sie aus der XML-Datei herausfiltern, die beim JPEG-Export aus dem TUFF-Viewer erzeugt wird. Bezeichnet man deren Eckpunkte ausgehend vom linken unteren Punkt mathematisch umlaufend mit P1 – P4, so gilt für deren untere und obere Begrenzungslinie: [math]\displaystyle{ y = y_1 + \frac {y_2 - y_1}{x_2 - x_1} (x - x_1) = y_1 + m_1 (x - x_1)\\ y = y_4 + \frac {y_3 - y_4}{x_3 - x_4} (x - x_4) = y_4 + m_2 (x - x_4) }[/math] Der Fluchtpunkt liegt nun im Schnitt der beiden Linien: [math]\displaystyle{ x_f = \frac {(y_1 - m_1 x_1) - (y_4-m_2 x_4)} {m_2 - m_1} }[/math] Analog kann man ggf. den Fluchtpunkt der Fahrbahn aus jeweils zwei Fluchtpunkten auf den Fahrbahnrändern errechnen.

Brennweite

Die Brennweiten [math]\displaystyle{ f }[/math] der für das Poliscan-Speed zulässigen Objektive betragen 25 mm, 35 mm, 50 mm und 75 mm. Auf dem Gerät sind jeweils zwei Kameras montiert; ein gut geführtes Messprotokoll protokolliert deren Brennweiten. In den Messdaten selbst ist die Brennweite des Fotos nicht protokolliert, sondern einzig die verwendete Kamera, nämlich Cam0 für Kamera 1 und Cam1 für Kamera 2. Die oben genannten Brennweiten lassen sich mittels der Pixelgröße von 7,4 µm direkt in Pixel und horizontalen Objektivöffnungswinkel (HFOV = horizontal field of view) umrechnen:

  • 25 mm = 3378 px (33,72°)
  • 35 mm = 4729 px (24,43°)
  • 50 mm = 6756 px (17,24°)
  • 75 mm = 10135 px (11,54°)

Verwenden eines Bildausschnitts

Bei der Berechnung von [math]\displaystyle{ \varphi }[/math] fließt der Abstand [math]\displaystyle{ x }[/math] zur Bildmitte in die Berechnung ein, sodass das Zentrum des ursprünglichen Bildes bekannt sein muss. Daher kann man Bildausschnitte nur dann verwenden, wenn man zuvor die Bildmitte markiert hat. Man kann nicht einfach den Abstand zur Mitte des Bildausschnitts verwenden! Verwendet man anstelle von [math]\displaystyle{ R' }[/math] schlicht den Abstand der Frontmitte (Nummernschildmitte) [math]\displaystyle{ R }[/math], so lässt sich problemlos auch ein Bildausschnitt verwenden.

Screenshots (skalierter Bilder)

Die Originalfotos werden in einem Sonderformat gespeichert und können nur mit dem herstellerspezifischen, recht teuren TUFF-Viewer betrachtet werden. In den gekrypteten Originaldateien wird das Bild zusammen mit den Begleitinformationen gespeichert. Bearbeitet man solche Fälle nur sporadisch, ist es sinnvoller, sich die Dateien im JPEG-Format zusenden zu lassen. Beim Export werden die Begleitinformationen dann als XML-Dateien mit gleichem Namen gespeichert. Allerdings ist nicht in allen Bußgeldstellen / Polizeidienststellen die dazu nötige Vorgehensweise bekannt, sodass öfters Screenshots oder anderweitig skalierte Fotos übersendet werden. (Das Originalformat beträgt 2048 × 2228 Pixel. Die Fotos sind oben und unten mit einem jeweils 100 Pixel hohen schwarzen Balken versehen, in den die Zusatzinformationen eingeblendet werden, sodass für das eigentliche Bild nur 2048 × 2028 Pixel übrig bleiben.)

Muss man mit (meist) herunterskalierten Fotos arbeiten, so ist deren Pixelgöße entsprechend größer. Außerdem muss die Zeilenauslesezeit angepasst werden, denn diese "größeren" Pixel werden entsprechend langsamer ausgelesen. Danach verläuft die Berechnung jedoch völlig analog.

Warum verlaufen die Leuchtspuren gekrümmt?

Im Beispielfoto oben auf der Seite verlaufen die Leuchtspuren gekrümmt; ihre Steigung wird zum unteren Bildrand hin flacher. Dieser Effekt ist auf jedem solchen Foto zu beobachten, egal ob Rechts- oder Linksmessung. Er beruht darauf, dass sich das Fahrzeug nach der Aufnahme weiterbewegt und der Winkel [math]\displaystyle{ \varphi' }[/math] Leuchtquellen dabei ständig zunimmt, sodass der Term [math]\displaystyle{ 1 / \sin \varphi' }[/math] mit der Zeit größer wird. (Der Term [math]\displaystyle{ \cos \varphi / \cos \varphi' }[/math] verändert sich hingegen kaum.)

Anschaulicher gesagt: Je größer der Winkel [math]\displaystyle{ \varphi' }[/math], umso größer ist diejenige Komponente der Fahrzeuggeschwindigkeit, die in Horizontalrichtung des CCD-Chip zeigt und die Geschwindigkeit [math]\displaystyle{ v_x }[/math] bewirkt.

Weitere Beiträge zum Thema im VuF

zu Laser:

Weitere Infos zum Thema

Weitere Infos zum Thema

Abgerufen von „http:///wiki/index.php?title=Auswertung_der_Leuchtspuren_in_Messfotos&oldid=25558“